Betaspektrum.

 

Øvelsens formål er at bestemme energierne for b-partikterne fra Sr-90 ved at afbøje dem 90o

i et magnetfelt.

 

Teori:

Når en kerne henfalder ved en b-proces, udsendes der dels en elektron, dels en antineutrino.

Den frigivne energi, deles mellem de tre partikler kernen, elektronen og antineutrinoen.

Når en elektron med hastigheden v og ladningen -e bevæger sig vinkelret på feltlinierne i et homogent magnetfelt B, beskriver den en cirkulær bane med radius r.

Lorentzkraften      leverer den nødvendige centripetalkraft.

Der gælder altså:

 

                                                   Û

 

 

 (*)                                            = impulsen

 

 

Hvis elektronerne er langsomme, kan vi regne klassisk, og den energien er bestemt ved:

 

                                     

 

Hvis derimod elektronerne er hurtige, må der regnes relativistisk 

Der gælder da følgende formel for energien:

 

 (**)                          

 

her er mo =      =      elektronens hvilemasse

          c = lysets fart

          r = radius i cirkelbuen  (i SI enheder)

         B = magnetfeltets størrelse


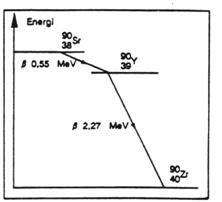
Figur 1   energiniveaudiagram       

                                                  

Relativitetsteori:

I relativitetsteorien lærer vi , at partikler i bevægelse har større masse end de samme partikler når de er i hvile. Man indfører derfor begreberne hvilemasse og vandremasse.

Når partiklerne bevæger sig med hastigheden v, er dens vandremasse m ifølge relativitetsteorien givet ved:

(***)                                     , hvor mo er hvilemassen.

 

Der gælder nu Einsteins formel :          Û        

 

Betragt     (***)           Û   

 

                                    Û      

indsættes udtrykket fra (*) fås

 

                                  

 

Der indsat i Einsteins formel giver  (**)

 

 

 

 

Apparatur:

b-kilde (tag den nyeste fra 1982)

Betaspektrums- plastikholder til kilden

to spoler med 600 vindinger , og med en lukket jernkerne (dog med et luftgab til plastikholderen)

strømforsyning (feks type ES 11.17)  og amperemeter

Hall-sonde med tilhørende generator, og voltmeter tilsluttet      (magnetfeltmåler)

GM-rør.

 

 

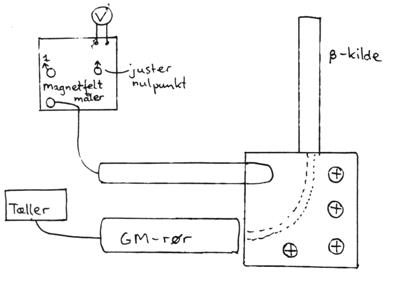
Opstilling fortsat:

 

 

 

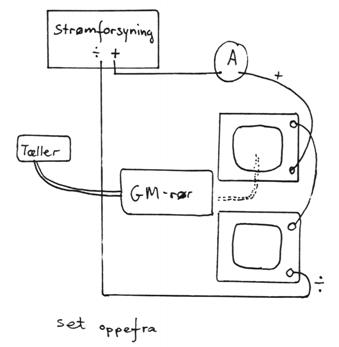
Start med at forbinde ledningerne til jernkernen som vist ovenfor.

Check  med højrehåndsreglen at afbøjningen sker den rigtige vej.

Amperemeteret sættes i kredsen for sikre at strømmen I holdes under 2A, (mere kan spolerne ikke tåle).

Magnetfeltet frembringes nu af elektromagneten.

Mål radius i cirkelbuen  og tilføj  kilden .

GM-røret indstilles til at tælle i 60 sekunder. Hætten tages af.

b-partiklerne sendes ind i magnetfeltet, hvorved de afbøjes i cirkelbaner, hvis radier afhænger af partiklernes energier.

De  b-partikler, der afbøjes netop 90o,rammer GM-røret og tælles.

Hall-sonden sættes i stativ for at undgå at den knækker.

Voltmeteret sættes så det måler i området 0-2V  (2DCV), idet 1V~1T.

Generatoren sættes på : 1,  og der drejes på justeringsknappen således at magnetfeltet er 0,

når sonden er parallel med jordens magnetfelt.

Mål nu baggrundsstrålingen   N0   , mens kilden er i, og strømmen er nul.

Skru nu op på strømmen og iagttag  ( blot ved at lytte til geigertælleren) at  tælletallet stiger,

(gør det ikke det er der noget galt med din opstilling).

 

Indstil nu magnetspolestrømmen , mål den magnetiske induktion B med Hallsonden, og mål tælletallet med GM-tælleren.

Indstil på en ny værdi af spolestrøm og mål igen.

Noter resultaterne i skema.

Prøv om I kan finde to toppe svarende til de to henfald .

 

B/ T

0,04

0,05

0,06

0,07

0,08

0,09

0,1

0,11

0,12

N

 

 

 

 

 

 

 

 

 

N-No

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

 

 

 

 

                                                                            

B/T

0,13

0,14

0,15

0,16

0,17

0,18

0,19

0,20

0,21

N

 

 

 

 

 

 

 

 

 

N-No

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

 

 

 

 

 

B/T

0,22

0,24

0,26

0.28

0,3

0,32

0,34

 

 

N

 

 

 

 

 

 

 

 

 

N-No

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

 

 

 

 

 

Usikkerheden på tælletallene er   , udregn den største usikkerhed ud fra det største tælletal.

Udvælg en af de målinger, der svarer til den største partikelenergi

            (størst B og tælletal større end No).

Indsæt data i (*) og udregn elektronens hastighed  (her regner vi ikke relativistisk).

Sammenlign denne fart med lysets fart.

Kan det gå an at benytte de klassiske formler eller skal vi regne relativistisk?

 

Udregn nu E  og tegn en   (E,N) graf. (****)

Kommenter grafen, og giv et skøn over b-partiklernes maksimale energi.

Hvad betyder det at grafen har et maksimum?

Kan man se på kurven at der er to forskellige b-henfald i kilden?

 

 

Kommentar: Teoretisk set skulle en bestemt værdi af B svare til, at elektroner med en bestemt energi når frem til tælleren. Elektroner med en højere energi vil ikke blive afbøjet tilstrækkeligt, og elektroner med en lavere energi  vil blive afbøjet for meget. På grund af tællerens og kildens udstrækning vil tælleren modtage elektroner inden for et vist interval.  (E,N)- grafen giver derfor kun en tilnærmelse til energifordelingen.

 

Og så er det ikke helt korrekt for:

(****) Fordelingen er statistisk med en kendt øvre grænse.

For såvidt angår fordelingen skal man passe  på - det er formelt set en fordeling i p (bevægelsesmængde), idet magnetfeltet netop sorterer efter denne størrelse, ikke energien. Når man ud fra denne fordeling vil lave en energifordeling, skal der multipliceres med en faktor dp/dE for hvert energiinterval. Fordelingen kommer derfor til at se lidt anderledes ud end den målte fordeling og maksimum flytter sig også.

 

EH 16-03-2005